Some Step by Step Proofs

Andy Novocin

Daily Challenge 1 Solution

Original: If \(x^2 = x+1\) then \(x = 1 + \sqrt{5}\) or \(x = 1 - \sqrt{5}\)

Converse: If \(x = 1 + \sqrt{5}\) or \(x = 1 - \sqrt{5}\) then \(x^2 = x + 1\)

Contrapositive: If \(x \neq 1 + \sqrt{5}\) and \(x \neq 1 - \sqrt{5}\) then \(x^2 \neq x + 1\)

A Pigeonhole Proof

Given \(n\) objects and \(k < n\) containers which hold them. Prove that at least one container has more than one object.

• Proof: Suppose not.
• (That means that \(k < n\) and all containers have one or less objects.)
• Let \(n_i\) be the number of objects in container \(i\).
• Then \( n = n_1 + \ldots + n_k \).
• For each \(i\) we know \(n_i \leq 1\) (based on our supposition)
• Thus \(n = n_1 + \ldots + n_k \leq k < n\).
• That implies that \(n < n\) which is a contradiction.

Daily Challenge 2 Solution

If \(x^3\) is irrational then \(x\) is irrational.

We will prove the contrapositive.

Let \(x = \frac{m}{n}, n \neq 0\) for \(n,m\in\mathbb{Z}\).

Then \(x^3 = \frac{m^3}{n^3}\).

But \(m^3, n^3 \in \mathbb{Z}\) and \(n^3 \neq 0\) so \(x^3\) is rational.

Let \(n\) be an integer. Prove that \(9n^2 + 3n -2\) is even.

• Proof: Solve first for evens, then for odds.
• EVENS: Let \(n = 2k\) for some \(k\).
• \(9 (2k)^2 + 3(2k) -2 = 36k^2 + 6k - 2\)
• \( = 2(18k^2 + 3k -1) \) which is even.
• ODDS: Let \(n = 2k + 1\) for some \(k\).
• We explore: \(9 (2k + 1)^2 + 3(2k + 1) -2 \)
• \( = 36k^2 + 36k + 9 + 6k + 3 - 2 \)
• \( = 36k^2 + 42k + 10 = 2(18k^2 + 21k + 5)\) even

ICUP

Let \(a\) and \(b\) be integers. Explore \(a\) is even and odd, \(b\) is even and odd.

Find a necessary and sufficient condition for \(a^2 - b^2\) to be odd.

Can you prove it?

Show that \(\sqrt{2}\) is irrational

• Proof: Suppose not.
• Let \(\sqrt{2} = \frac{m}{n}\)
• Without loss of generality we can say only one of \(m\) and \(n\) are even (remove common factors)
• Now \( 2 = \frac{m^2}{n^2}\) which is \(2n^2 = m^2\)
• That means that \(m^2\) is even.
• An odd number squared is odd, so \(m = 2k\) for some \(k\).
• Replacing: \(2n^2 = 4k^2\).
• Simplifying: \(n^2 = 2k^2\).
• This implies that \(n\) is also even.
• A contradiction.

Pythagorean Theorem \(a^2 + b^2 = c^2\)

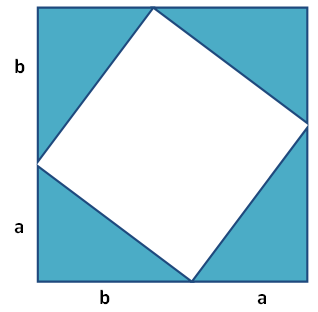
\( (a+b)^2 = 4(ab/2) + c^2 \)

\( a^2 + b^2 + 2ab = 2ab + c^2 \)

ICUP

Show that the product of an irrational and an irrational is irrational.

Counter-Example \(\sqrt{2} \sqrt{2} = 2\)

Theorem: There exists two positive irrational numbers, \(s, t\) such that \(s^t\) is rational.

Proof:

Look at \(\sqrt{2}^{\sqrt{2}}\).

Case 1: It is rational. Then let \(s = t = \sqrt{2}\).

Case 2: It is irrational. Then let \(s = \sqrt{2}^{\sqrt{2}}\) and \(t = \sqrt{2}\).

Notice that \(s^t = {(\sqrt{2}^{\sqrt{2}})}^{\sqrt{2}} = \sqrt{2}^2 = 2\)