April 27th

Graph Vocabulary Terms

• A graph is a pair of sets \(V, E\), vertices and edges. In our book we specify that \(V\) is non-empty and \(E \subseteq V \times V\) does not allow elements (edges) of the type \((v,v)\) (loops).
• An edge \(e = (u,v) \in E\) can be denoted \( e = uv\) while \(u\) and \(v\) are the ends (or end vertices) of \(e\). It is said that \(e\) joins \(u\) and \(v\).
• We say that \(u\) and \(v\) are incident with edge \(uv\).
• Two vertices are adjacent if they are end vertices of the same edge (an edge joins them).
• Two edges are adjacent when they have a common vertex.
• The number of edges incident with a vertex is the degree of that vertex, denoted \(\deg{v}\).
• A vertex of even (odd) degree is called an even (odd) vertex.
• A vertex of degree 0 is isolated
• A pseudograph allows multiple edges and loops.
• \(G_1(V_1, E_1)\) is a subgraph of \(G(V,E)\) if and only if \(V_1 \subseteq V\) and \(E_1 \subseteq E\).
• The complete graph on \(n\) vertices is denoted \(K_n\) and has the property that every two vertices are adjacent.
• A bipartite graph is one where the vertices can be partitioned into two sets \(V_1\) and \(V_2\) in such a way that every edge joins a vertex in \(V_1\) to a vertex in \(V_2\). (Note that there are no edges within \(V_1\) or \(V_2\).)
• A complete bipartite graph is one in which every vertex in \(V_1\) is joined to every vertex in \(V_2\). This is denoted \(K_{n,m}\) when \(|V_1| = n\) and \(|V_2| = m\).
• Let \(d_1, \ldots, d_n\) be the degree of the vertices of a graph \(G\) ordered so that \(d_1 \geq d_2 \geq \cdots \geq d_n\). This is called the degree sequence of a \(G\).
• The sum of the degrees of any graph (or pseudograph) is \(2 |E|\) (credited to Euler). This implies that the number of odd vertices is even.
• The notation \(G \setminus {e}\) or \(G \setminus {v}\) represent the subgraph of \(G\) formed by removing \(e\) or \(v\) (and all edges incident with \(v\)).

The problem set

1. Draw all possible graphs on three vertices. How many edges are there in each graph? What are the degree sequences? Can you do this on pseudographs?
2. Draw \(K_7, K_{3,4}, K_{2,6}\).
3. For each of these degree sequences either draw the graph or explain why no such graph exists:
   • \(100, 99, 98, \ldots 3, 2, 2, 2\)
   • \(1,1,1,1,1,1\)
   • \(6,6,4,2,2,2,1,1\)
   • \(5,4,3,2,1,1\)
   • \(4,3,2,2,1\)
4. How many complete bipartite graphs are there with \(n\) vertices?
5. Does there exist a graph with five vertices, every vertex incident with at least one edge, but no two edges adjacent? Explain.
6. Is this graph bipartite?

   ---

   
7. How about this one?

   ---

   
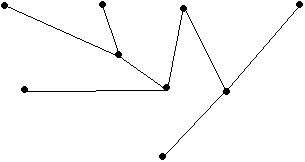
8. * (next DC) Can you come up with a general method for this?
9. Let \(G_0\) be the graph from problem 6. Draw \(G_0 \setminus {f}\). Draw \(G_0 \setminus {ab}\).

Follow up to the derangement video. (Since today is so literal.)